R 예제 코드 - Logistic Regression / 로지스틱 회귀분석
로지스틱 회귀분석을 drama_genre.csv 데이터에 적용해서 genre를 분류하는 R 코드를 만들어 보자.
▼ 로지스틱 회귀분석 알고리즘에 대한 이론적인 설명이 궁금하다면? ▼
2017/03/21 - [Analysis/ALGORITHM] - Logistic Regression / 로지스틱 회귀분석
1. 데이터 준비하기
아래에서 drama_genre.csv 데이터를 다운로드 한다. 이 데이터는 iris 데이터를 약간 변형식켜서 만든 샘플 데이터이다.
다운로드 받았으면 csv 파일을 불러온다. 경로는 csv 파일을 저장했던 폴더로 지정한다. \가 아닌 / 를 사용하는 것에 주의하자.
data <- read.csv(file = "D:/R/kkokkilkon/drama_genre.csv")
2. 데이터 확인하기
다운로드 받았던 데이터가 어떤 형태인지 확인하자.
summary(data)
이 데이터는 3개 변수로 이루어져 있는데 각 변수의 의미는 아래와 같다.
sum_age_mainactors : 주연배우 나이 합계
avg_slap_face : 회 평균 뺨 맞는 횟수
genre : 드라마 장르
▼ 만약에 설명변수에 범주형 변수가 있다면 더미변수로 변환하기 ▼
2017/03/28 - [Analysis/ALGORITHM] - Dummy Variable / 더미변수 / 가변수
3. 데이터 필터링 하기
현재 genre 변수는 3가지 카테고리를 가진다. 로지스틱 회귀분석을 적용하기 위해서는 2가지 카테고리만 가져야 하므로 청소년드라마를 제외하고 막장드라마와 멜로드라마 데이터만 필터링 하자.
# 데이터 필터링
data <- subset(data, genre %in% c("막장드라마", "멜로드라마"))
# factor의 레벨을 3에서 2로 바꾸어 주기 위함줄여주기 위함
data$genre <- as.factor(as.character(data$genre))4. 데이터 분포 보기
필터링한 데이터의 분포가 어떠한지 시각적으로 확인해보자.
# 색 투명도 설정을 위한 alpha 함수를 사용하기 위해 scales 패키지를 설치하고 라이브러리 불러오기
install.packages("scales")
library(scales)
# 산점도 그리기
plot(formula = sum_age_mainactors ~ avg_slap_face,
data = data,
col = alpha(c("blue", "green"), 0.8)[data$genre],
xlab = "회당 뺨 맞는 횟수",
ylab = "주연배우 나이 합계",
main = "드라마 장르 분포")
# 범례 그리기
legend("topleft",
legend = levels(data$genre),
pch = 1,
col = alpha(c("blue", "green"), 0.8),
cex = 0.9,
bty = "n")5. 데이터 나누기 (train set, validation set, test set)
k-Fold Cross Validation을 할 예정이다. 여기서 k는 3으로 정하고 먼저 ( train + validation ) 과 test data 를 6 : 4 로 나눠보자.
# 재현성을 위한 seed 설정
set.seed(9876)
# idx 설정 (6 : 4)
idx <- sample(x = c("train_valid", "test"),
size = nrow(data),
replace = TRUE,
prob = c(6, 4))
# idx에 따라 데이터 나누기
train_valid <- data[idx == "train_valid", ]
test <- data[idx == "test", ]
# test 데이터 설명변수/반응변수 나누기
test_x <- test[, -3]
test_y <- test[, 3]6. train_valid와 test 데이터 분포 확인하기
산점도를 그려서 train_valid, test 데이터의 분포를 확인해보자.
# alpha 함수를 사용하려면 미리 scales 라이브러리를 불러와야 한다.
library(scales)
# train_valid 산점도 그리기
plot(formula = sum_age_mainactors ~ avg_slap_face,
data = train_valid,
col = alpha(c("blue", "green"), 0.8)[train_valid$genre],
pch = 0,
main = "드라마 장르 분포",
xlab = "회당 뺨 맞는 횟수",
ylab = "주연배우 나이 합계")
# test 데이터 표시하기
points(formula = sum_age_mainactors ~ avg_slap_face,
data = test,
pch = 16,
cex = 1.2,
col = alpha(c("blue", "green"), 0.5)[test$genre])
# 범례 그리기
legend("topleft",
c(paste0("train_valid ", levels(train_valid$genre)), paste0("test ", levels(test$genre))),
pch = c(0, 0, 16, 16),
col = c(alpha(c("blue", "green"), 0.8), alpha(c("blue", "green"), 0.5)),
cex = 0.9,
bty = "n")7. Cross Validation 결과 테이블 생성하기
k-Fold Cross Validation 후 분류 정확도를 저장할 결과 테이블을 미리 생성한다.
fold : k-Fold에서 k의 횟수
mdl : 회귀모델의 종류 (full과 step 두가지를 만들 예정임)
i : 분류 임계치 (0부터 1까지 0.025 단위로 시퀀스를 만듬)
accuracy : 분류 정확도 (NA로 넣어두고 나중에 분류 정확도를 계산해서 입력할 예정)
result <- data.frame(fold = rep(c(1, 2, 3), each = 82),
mdl = rep(c("full", "step"), 41),
i = rep(seq(0, 1, length.out = 41), 6),
accuracy = rep(rep(NA, 41), 6))8. 3-Fold 적용하면서 로지스틱 회귀분석 모델 만들기
설명을 위해 스크립트를 끈어 쓰겠다.
반복문을 사용하여 3-Fold를 한다. k는 train_valid 데이터를 1 / 2 / 3 그룹으로 나누기 위해서 만들어진 값이다. k에 해당하는 데이터는 k 회차에서 valid 데이터가 되고 나머지 데이터들은 train 데이터가 된다. k 회차는 1회차부터 3회차까지 진행된다. (3-Fold 니까)
idx <- sample(x = c(1:3), size = nrow(data), replace = TRUE, prob = c(1, 1, 1))
for(k in c(1, 2, 3)){
# idx에 따라 train vs. valid 데이터 나누기
valid <- train_valid[idx == k, ]
train <- train_valid[idx != k, ]
# valid 데이터 설명변수/반응변수 나누기
valid_x <- valid[, -3]
valid_y <- valid[, 3]
로지스틱 회귀분석 모델을 생성하기 위해서는 glm 함수를 사용한다. 각 옵션의 의미는 아래와 같다.
formula : 회귀식 ( ~ 앞이 반응변수(y)이고, ~ 뒤가 설명변수(x)이다. 여기서 점( . )의 의미는 반응변수를 제외한 train 데이터의 모든 변수를 의미한다.)
data : train 데이터
family : glm 함수가 제공하는 회귀모델 중 어떤 회귀모델을 생성할 것인지를 결정하는 옵션. 로지스틱 회귀분석을 위해서는 family 옵션을 "binomial"로 주어야 한다.
# 로지스틱 회귀분석 모델 생성
full <- glm(formula = genre ~ .,
data = train,
family = "binomial")
# Stepwise
step <- step(object = full,
trace = F)
# full과 step 모델별 확률 예측
full_pred_p <- as.numeric(predict(object = full,
newdata = valid_x,
type = "response"))
step_pred_p <- as.numeric(predict(object = step,
newdata = valid_x,
type = "response"))
분류 정확도를 계산하기 위해 predict 된 확률값을 임계치를 기준으로 level 1 또는 2로 분류한 후 실제 관측값과 비교하여 분류가 정확한 비율을 계산한다.
# 분류 정확도의 분모
l <- length(valid_y)
for(i in unlist(unique(result$i))){
# i를 기준으로 0 또는 1로 분류
full_pred_class <- ifelse(full_pred_p < i, levels(valid_y)[1], levels(valid_y)[2])
step_pred_class <- ifelse(step_pred_p < i, levels(valid_y)[1], levels(valid_y)[2])
# 분류 정확도 계산
full_accuracy <- sum(full_pred_class == valid_y) / l
step_accuracy <- sum(step_pred_class == valid_y) / l
# result 테이블에 분류 정확도 입력
result[result$fold == k
& result$mdl == "full"
& result$i == i, "accuracy"] <- full_accuracy
result[result$fold == k
& result$mdl == "step"
& result$i == i, "accuracy"] <- step_accuracy
}
}
step은 Stepwise 단계적 변수 선택법을 해주는 함수로, AIC가 작아지는 방향으로 변수를 선택한다. trace는 변수 선택하는 과정을 Console에 출력할지 여부이다. (F는 출력을 안 한다는 의미임)
# Stepwise
step <- step(object = full,
trace = F)
생성한 full과 step 두 모델을 가지고 확률을 예측한다.
type 옵션의 디폴트 값은 "link"인데 type이 "link"인 경우 결과가 로그오즈로 출력되고, "response"인 경우에는 확률로 변환해서 출력된다.
아까 반응변수로 factor 변수인 genre를 넣었는데, 어떤 카테고리가 0이고 어떤 카테고리가 1인지 궁금할 것이다. (정해준 적이 없으니까^^;;)
levels(반응변수)를 했을 때 나오는 순서대로 0, 1 이다. 즉, level 1인 변수가 0이고, 2인 변수가 1이다. 이 데이터에서는 levels(data$genre)를 하면 나오는 순서가 막장드라마, 멜로드라마 순이므로 막장드라마가 0이고 멜로드라마가 1이다. 따라서 아래 코드에서 나온 결과는 멜로드라마일 확률을 의미한다.
# full과 step 모델별 확률 예측
full_pred_p <- as.numeric(predict(object = full,
newdata = valid_x,
type = "response"))
step_pred_p <- as.numeric(predict(object = step,
newdata = valid_x,
type = "response"))이제 분류 정확도를 계산해보자. (분류 정확도 = 정답건수 / 전체건수)
임계치 i를 0부터 1까지 0.025 단위로 증가시키면서 분류 정확도가 어떻게 바뀌는지 반복해보는 코드이다.
# 분류 정확도의 분모
l <- length(valid_y)
for(i in unlist(unique(result$i))){
# i를 기준으로 0 또는 1로 분류
full_pred_class <- ifelse(full_pred_p < i, levels(valid_y)[1], levels(valid_y)[2])
step_pred_class <- ifelse(step_pred_p < i, levels(valid_y)[1], levels(valid_y)[2])
# 분류 정확도 계산
full_accuracy <- sum(full_pred_class == valid_y) / l
step_accuracy <- sum(step_pred_class == valid_y) / l
# result 테이블에 분류 정확도 입력
result[result$fold == k
& result$mdl == "full"
& result$i == i, "accuracy"] <- full_accuracy
result[result$fold == k
& result$mdl == "step"
& result$i == i, "accuracy"] <- step_accuracy
}
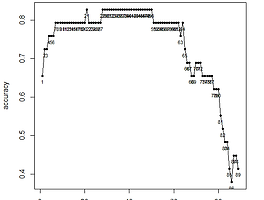
}9. 임계치 i에 따른 모델별 k별 분류 정확도 그래프 그리기
선형 그래프를 그릴 것이기 때문에 반드시 정렬이 필요하다.
이제 full k = 1~3, step k = 1~3 이렇게 6개 그래프를 그려보겠다.
# full 모델 k-Fold = 1
plot(accuracy ~ i,
result[result$mdl == "full" & result$fold == 1, ],
type = "l",
col = alpha("purple", 0.4),
ylim = c(0.3, 1),
xlab = "임계치",
ylab = "분류 정확도",
main = "분류 정확도 in full/step 3-Fold CV")
# full 모델 k-Fold = 2
lines(accuracy ~ i,
result[result$mdl == "full" & result$fold == 2, ],
col = alpha("orange", 0.4))
# full 모델 k-Fold = 3
lines(accuracy ~ i,
result[result$mdl == "full" & result$fold == 3, ],
col = alpha("green", 0.4))
# step 모델 k-Fold = 1
lines(accuracy ~ i,
result[result$mdl == "step" & result$fold == 1, ],
col = alpha("purple", 0.5),
lty = 2)
# step 모델 k-Fold = 2
lines(accuracy ~ i,
result[result$mdl == "step" & result$fold == 2, ],
col = alpha("orange", 0.5),
lty = 2)
# step 모델 k-Fold = 3
lines(accuracy ~ i,
result[result$mdl == "step" & result$fold == 3, ],
col = alpha("green", 0.5),
lty = 2)
# 범례 그리기
legend("topleft",
c("full k=1", "full k=2", "full k=3",
"step k=1", "step k=2", "step k=3"),
col = c(alpha(c("purple", "orange", "green"), 0.4),
alpha(c("purple", "orange", "green"), 0.5)),
lty = rep(c(1, 2), each = 3),
bty = "n",
cex = 0.9)10. 모델별 임계치 i에 따른 평균 분류 정확도 그래프 그리기
이제 full과 step 각각의 평균 분류 정확도를 계산해보자. ddply 함수는 데이터를 그룹핑해준다. mdl, i별 accuracy의 평균을 계산한다.
# 그룹핑을 위해 plyr 패키지를 설치하고 라이브러리 불러오기
install.packages("plyr")
library(plyr)
# 모델별 임계치별 평균 분류 정확도 계산하기
tmp <- ddply(result, .(mdl, i), summarise, avg_accuracy = mean(accuracy))이제 아까 그렸던 분류 정확도 그래프 위에 평균 분류 정확도를 그려보자.
# full 모델
lines(avg_accuracy ~ i,
tmp[tmp$mdl == "full", ],
col = alpha("red", 0.7),
lty = 1,
type = "o",
pch = 20)
# step 모델
lines(avg_accuracy ~ i,
tmp[tmp$mdl == "step", ],
col = alpha("red", 0.7),
lty = 2,
type = "o",
pch = 20)
# 범례 그리기
legend("topright",
c("full avg accuracy", "step avg accuracy"),
pch = 20,
col = alpha("red", 0.7),
lty = rep(c(1, 2)),
bty = "n",
cex = 0.9)평균 분류 정확도가 가장 높은 임계치는 0.4에 가까운 부분이다. 정확한 임계치가 얼마인지 출력해보자.
tmp[tmp$avg_accuracy == max(tmp$avg_accuracy), ]
validation 결과, 분류 정확도는 step 모델을 사용해서 임계치 i = 0.45 로 분류했을 때 가장 정확했고 분류 정확도는 74.8% 라고 해석할 수 있다.
11. test 데이터로 분류 정확도 계산하기
아까 나눠놨던 test_x 데이터를 step 모델과 임계치 0.45를 이용해 막장드라마와 멜로드라마로 분류해보고 test_y와 비교해보자.
# test_x가 멜로드라마일 확률을 step 모델로 구하기
test_p <- as.numeric(predict(object = step,
newdata = test_x,
type = "response"))
# 임계치 0.45를 기준으로 막장드라마와 멜로드라마 분류하기
test_class <- ifelse(test_p < 0.45, levels(data$genre)[1], levels(data$genre)[2])
# 분류 정확도 계산하기
sum(test_class == test_y) / length(test_y)test 데이터의 분류 정확도는 80.6%로 valid 데이터보다 더 높은 수치가 나왔다. (다행이도ㅋㅋ)
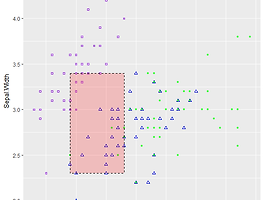
12. test 데이터로 분류 결과 산점도 그리기
test 데이터가 train_valid 데이터 대비 어떻게 분류되었는지 시각적으로 표현해보자.
# 정답/오답 만들기 (pch 옵션을 위해)
ox <- as.factor(ifelse(test_class == test_y, "O", "X"))
# train_valid 산점도 그리기
plot(formula = sum_age_mainactors ~ avg_slap_face,
data = train_valid,
col = alpha(c("blue", "green"), 0.8)[train_valid$genre],
xlab = "회당 뺨 맞는 횟수",
ylab = "주연배우 나이 합계",
main = "드라마 장르 분포")
# test 산점도 그리기
points(formula = sum_age_mainactors ~ avg_slap_face,
data = test,
col = alpha(c("blue", "green"), 0.6)[test$genre],
pch = c(19, 17)[ox])
# 범례 그리기
legend("topleft",
legend = c(paste0("train_valid ", levels(train_valid$genre)),
paste0("test ", levels(test$genre), " 정답"),
paste0("test ", levels(test$genre), " 오답")),
pch = c(1, 1, 19, 19, 17, 17),
col = c(alpha(c("blue", "green"), 0.8),
alpha(c("blue", "green"), 0.6),
alpha(c("blue", "green"), 0.6)),
cex = 0.9,
bty = "n")위 그래프만 보면 이 데이터가 로지스틱 회귀분석으로 어떻게 분류되었는지 손쉽게 파악할 수 있다. 또한 train_valid 데이터가 섞여있는 가운데 부분에서 오분류가 주로 발생한 것도 알 수 있다. (그래서 train 데이터가 중요하다!)
#Algorithm#Analysis#bigdata#classification#csv샘플#csv샘플데이터#csv파일#data#logistic#logisticregression#machinelearning#ML#r#rsourcecode#rstudio#r샘플#r샘플데이터#r예제#R코드#sampledata#데이터분석#로지스틱리그레션#로지스틱회귀분석#머신러닝#분류#분류문제#분류정확도#분석#빅데이터분석#샘플데이터#알고리즘#정확도#지도학습
'회사생활 > R' 카테고리의 다른 글
| party::cforest vs. randomForest::randomForest (0) | 2017.04.23 |
|---|---|
| 로컬에서 데이터 불러오기 / 데이터 저장하기 (0) | 2017.03.26 |
| 한눈에 정리하는 ggplot2를 이용한 R 시각화 기초 1 (2) | 2017.03.17 |
| [R 예제 코드] KNN / k-NN / k-Nearest Neighber / k-최근접 이웃 (4) | 2017.03.15 |
| Train vs. Validation vs. Test Data (0) | 2017.03.14 |
 drama_genre.csv
drama_genre.csv